Better With Age
Predicting mortality for post-level term insurance
Spring 2020Photo: Getty Images/Dimitri Otis
Actuaries have a long and storied history of providing the joint mathematical and business foundation for the insurance industry. Yet, advanced predictive analytics techniques with machine learning (ML) and artificial intelligence (AI) have not made it into the standard toolkit of the typical actuary. Insurers and actuaries could reap major strategic benefits if they were to significantly increase their use of these advanced predictive techniques. In this article, we focus on mortality and lapse studies as one example.
Post-level term (PLT) insurance presents a unique set of challenges when it comes to predicting mortality and lapse experience. After a set period of, say, 10 or 20 years when the policyowner paid level premiums, the premium will rise annually. Customers will be highly motivated to identify all of their other options. Healthier individuals will have good alternatives and lapse their policies; the less healthy ones will remain. The greater the premium increase, the greater this effect will be—resulting in the classic mortality spiral.
How can we get a good quantification of the interrelationship between premium increases and lapse and mortality experience? By building a predictive analytics model—more advanced than those previously developed1,2—to set lapse and mortality assumptions, and price and value PLT insurance. Our model will statistically integrate heterogeneous customer cohorts,3 improve credibility in cohorts with sparse claims data, and provide a more complete understanding of the impact of premium changes on mortality rates. We can only imagine the additional improvements to insurer pricing and financial reporting that could be achieved with broader applicability of these techniques beyond PLT.
Our PLT Model
Our PLT model comprises three advanced predictive methods:
1. An innovative application of a statistical multivariate framework to model PLT lapse and mortality. This multivariate model reflects the causal structure (and almost immediate impact) of PLT lapsation and premium changes on mortality (PLT causal structure4) and provides better guidance for setting PLT premiums. Taking the causal structure into consideration is especially important when answering predictive “what if” questions (e.g., what happens to mortality if we change premiums by X percent).5
Consistent with our plan to model the lapse rate as a major driver of the dependence of mortality rates on premium level, we make assumptions in our model about the underlying data-generating processes:
- Whether a policyholder lapses at the end of the level term period is a stochastic function of various characteristics such as age, gender, risk class, face amount and the change in premium.
- This function may include complex dependencies among variables. For example, the effect of different face amounts on lapsation may vary by age, gender and so on.
- The differences in both base and shock lapse among cohorts cause perceptible differences in mortality levels.
2. The statistical technique of “partial pooling” to increase the credibility of sparsely populated cohorts. This is especially important when the volume of available data (especially mortality data) differs substantially by cohort, leading to differences in credibility—including cohorts with very limited credibility.
Partial pooling is a principled middle ground between complete pooling, which fits a single model for the entire population and ignores variations, and no pooling, which fits a single model for each cohort and ignores similarities shared among cohorts. Partial pooling is also known as hierarchical partial pooling.
Partial pooling enables us to share information (borrowing strength) among cohorts, regularize6 our model and account for different cohort sizes without incorporating ad hoc solutions. The data for each observed cohort informs and adds credibility to the probability estimates for all of the other cohorts. The extreme estimates are driven toward the population mean (“shrinkage” in Bayesian statistics) with significant lessening of variability that may have been created by noise in the data. This phenomenon is closely related to the concept of bias-variance trade-off,7 in which the tightness of fit to the observed data is reduced, so the derived estimates serve as better predictors. Partial pooling leaves us with better estimates, reduced variability and improved credibility.
Partial pooling smooths mortality estimates, which by itself is not new in actuarial science—different graduation techniques have been developed and implemented over the years. The distinct advantage of partial pooling is that it achieves the same goal by explicitly sharing information among cohorts in a principled way (guided by domain knowledge and analysis of the data), and it can improve credibility in sparsely populated cohorts.
3. The integrative statistical approach of Bayesian inference8,9 to quantify differences in experience among cohorts with different exposure levels. The generative nature10 of Bayesian modeling enables the incorporation of expert knowledge into the models in the form of model structure and informed priors.11,12 Bayesian models produce crucial uncertainty estimates (unlike the point estimates supplied by more traditional maximum likelihood approaches) needed for informed decision-making—especially with sparse mortality data. We use Bayesian multivariate modeling of lapse and mortality, but we do not include a numerical comparison of the Bayesian and non-Bayesian approaches in this article due to space considerations.
There are two key elements of our mortality-lapse model. The first is a nonlinear regression lapse model inspired by previous Society of Actuaries (SOA) studies.13,14 We added partial pooling of parameters across cohorts to increase accuracy, credibility and predictability. We changed the link function of the model from log to logit to ensure per-cohort lapsation is bounded by the exposure (previously it was possible for the model to predict more lapses than exposures, i.e., an actual-to-expected ratio > 1).
The second key element of our model is that it is a Bayesian version of the Dukes MacDonald (DM) mortality model.15,16 In this version, we model the effectiveness parameter as a nonlinear function of the cohort characteristics (e.g., age, risk class, gender, etc.), use priors that reflect actuarial knowledge regarding plausible parameter values of G (e.g., a reasonable prior might put more weight on values of G closer to 1 than 0),17 and infer the posterior distribution of G from the data (the distributions over model parameters after conditioning on the data). We use the nonlinear regression lapse model previously described to estimate a distribution of lapse rates by cohort. Mortality is estimated by integrating over two variables: the joint distribution of base/shock lapse rates and the effectiveness parameter, thereby completing the mortality-lapse model.
Our Model in Action
To implement the model, parameters for both the lapse and mortality models were estimated using Stan, a state-of-the-art platform for statistical modeling and high-performance statistical computation.18 We validated the estimates Stan provided with both Bayesian model comparison methods, such as leave-one-out (LOO) and Watanabe–Akaike information criterion (WAIC),19 and actual-to-expected (A/E) ratios.
The SOA data20 we used for our modeling, consisting of 8,066 different customer cohorts, is summarized in Figure 1.
Figure 1: Experience Used in the Model
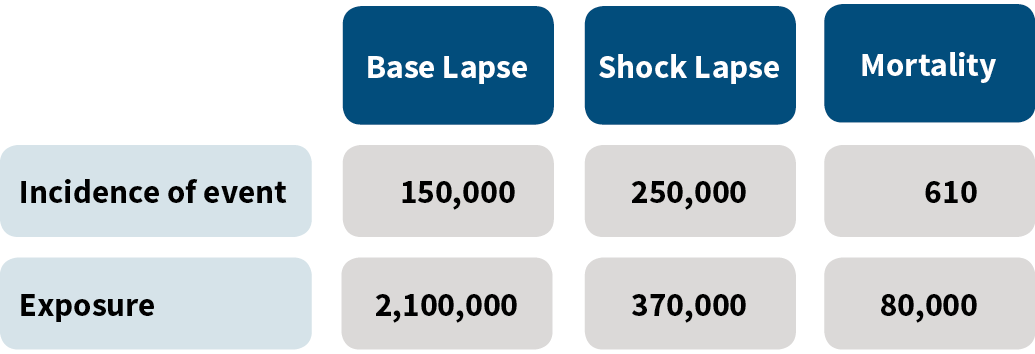
To quantify and validate the impact of the new Bayesian tools presented, we conducted an analysis. First, for the multivariate modeling of lapse and mortality, we examined three variants of DM mortality estimates:
- Assume fixed base lapse rates before the PLT period, fixed total lapse rates at the end of the level term period, and fixed effectiveness parameters. Optimal values for base and total lapse rates and the effectiveness parameter were found by using a standard gradient descent optimization algorithm. The lapse and effectiveness parameters do not vary by cohort though the select and point-in-scale mortality do vary by cohort.
- Empirically assess from the data both the base and total lapse rates by cohort. The effectiveness parameter was fixed. It was optimized using grid search.21
- Use a partially pooled model to estimate both base and total lapse rates that vary by cohort. The distribution of the effectiveness parameter was inferred from the data itself using NUTS,22 an adaptive extension of the Hamiltonian Monte Carlo Markov Chain algorithm.23
In each of these variants, expected mortality is computed based on the five input parameters to DM: effectiveness, base lapsation, shock lapsation, select mortality and point-in-scale mortality. The select and point-in-scale mortality used in the computation of expected mortality were selected from standard tables. We compared the actual deaths for each method in each cohort to the expected, and we then computed a weighted error as the mean absolute deviation of the predicted A/E ratio from an A/E ratio of 1, weighted by exposure. Figure 2 shows the results.24
Figure 2: Mean Absolute Deviation of Actual/Expected Ratios
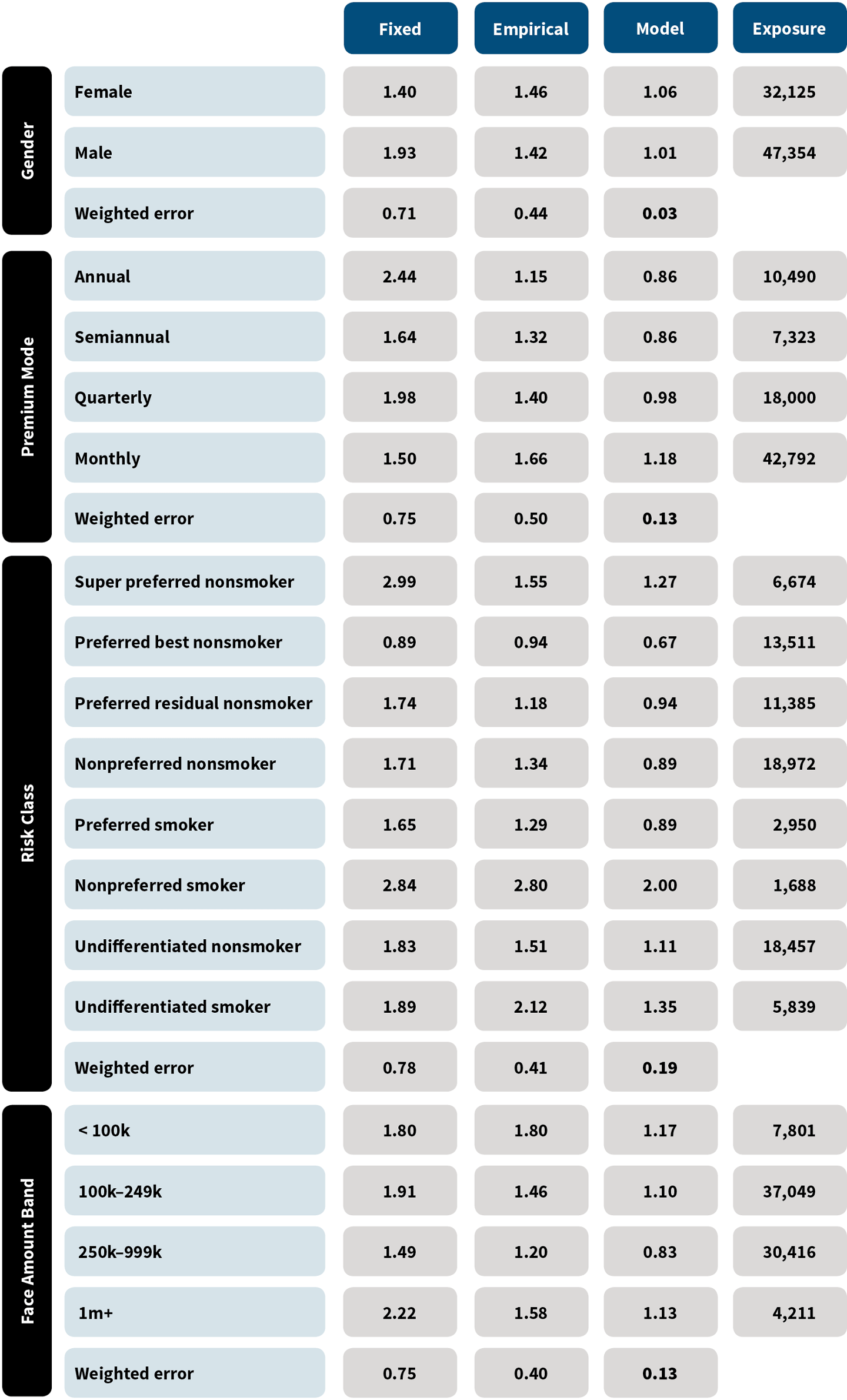
A model such as this can be continually improved. For example, we know mortality is often a bit higher for lower socioeconomic classes. Building in this knowledge may result in an A/E ratio closer to 1. Similarly, upper-income policyholders may have the ability to anti-select, which also could be built into the next model iteration. The Bayesian framework used is especially well-suited to the incorporation of this type of expert knowledge.
For partial pooling when measuring mortality rates, we fit a nonlinear regression model to publicly available mortality data25 with and without partial pooling of model parameters and held all else (e.g., the data and the characteristics being analyzed) constant. We compared the partially pooled model to both regularized and nonregularized nonlinear regression models using R’s glmnet package.
We ran the models with different characteristic subsets to validate that our results are not characteristic-dependent. Almost always, the models without partial pooling of parameters yielded implausible estimates for cohorts with especially low exposures or claims, sometimes deviating from the population mean by more than four orders of magnitude. On the other hand, the mortality rates in the partially pooled model were much closer to the population mean on an exposure-controlled basis. Outlier behavior of the magnitude seen when partial pooling was not used was not observed.
When comparing models using Bayesian selection methods,26 the partially pooled model had significantly better LOO cross validation and WAIC scores, as shown in Figure 3.27
Figure 3: Model Validation Comparison
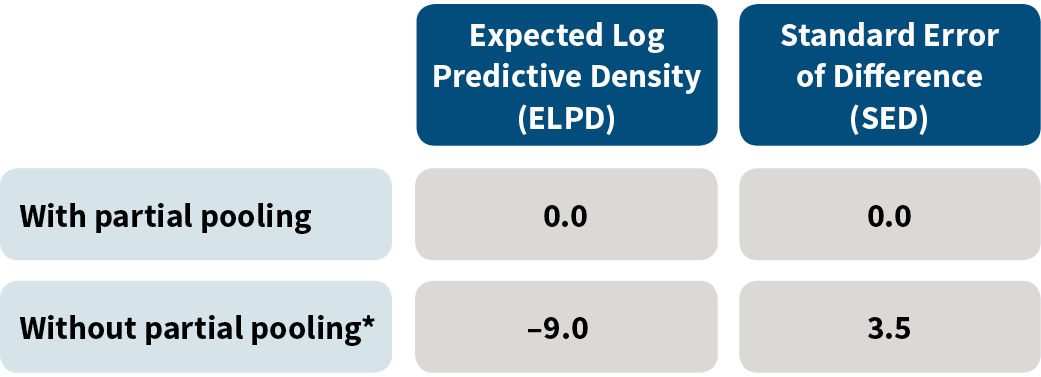
*For this row, we show values for the regularized (nonpartial pooling) model that gives the best results.
When predicting mortality rates for cohorts with relatively small exposures (~5 percent of the mean per-cohort exposure, 153 cohorts out of 8,000), the nonpooled models yielded mortality estimates that are less than 0.01 percent of the mean mortality rate (interestingly enough, over-estimation was not observed). This under-estimation resulted from improper handling of small sample sizes. These results held even with the regularized models, which are very similar to models with graduation.28
On the other hand, models with partial pooling did not produce such extreme estimates because of the beneficial impacts of shrinkage. Proper handling of mortality estimates in cohorts with small exposures is critical, as such cohorts will almost certainly exist when modeling data at high granularity.
Conclusion
This article explored innovative approaches to modeling PLT lapse and mortality. A multivariate PLT lapse and mortality model improves mortality estimates and sheds new light on the interactions among changes in premium, persistency and mortality. Because management would have the information it needs in real time, this transforms pricing, reserving and “what if” analysis.
Partial pooling shares information among cohorts, accounts for different cohort sizes, regularizes estimates and improves credibility. When there are multidimensional cohorts with sparse data, partial pooling can provide unique insights into policyholder behavior, which is very valuable for insurers looking to manage risks and finances and optimize top-line growth.
The Bayesian model allows us to capture our prior knowledge of the data-generating process, such as the reasonable values of the effectiveness parameter. Such a model will be practical and implementable—and not just a nice theoretical toy.
The methods discussed in this article are valuable for answering a wide range of sophisticated actuarial questions. Actuaries and insurers will want to consider how advanced methodologies such as the innovative lapse-mortality model, causal inference and Bayesian decision theory could be used to address crucial challenges. Now that the availability of computational resources facilitates the implementation of these advanced methodologies, insurers face a new imperative. These techniques can be extended to general lapse and mortality studies along with other aspects of the insurer experience. We look forward to seeing the improvements in pricing and reserving (such as for principles-based reserving) and the increases in credibility that will emerge from greater use of these techniques.
References:
- 1. Society of Actuaries. 2014 Post Level Term Lapse & Mortality Report. Society of Actuaries, 2014, (accessed January 27, 2020). ↩
- 2. Society of Actuaries. Lapse Modeling for the Post-Level Period—A Practical Application of Predictive Modeling. Society of Actuaries, 2015, (accessed January 27, 2020). ↩
- 3. In this article, a cohort means a group of policyholders who are the same age, gender, risk class, premium mode, face amount band and premium jump band. ↩
- 4. PLT causal structure means an in-depth understanding of the causal relationships between PLT pricing and experience. ↩
- 5. Due to space considerations, we do not include an in-depth causal analysis in this article. ↩
- 6. In this context, regularization means constraining model parameters, therefore reducing the risk of overfitting and improving the ability of the model to generalize. ↩
- 7. James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning With Applications in R. New York: Springer. ↩
- 8. A field of statistics in which uncertainty is quantified with probability, and quantities of interest are expressed as posterior expectations, taking into account prior/expert knowledge and how likely different models are given the observed data. ↩
- 9. Makov, U., A. Smith, and Y.-H. Liu. 1996. Bayesian Methods in Actuarial Science. Journal of the Royal Statistical Society. Series D (The Statistician) 45, no. 4:503–515. ↩
- 10. A generative model describes how a data set is generated in terms of a probabilistic model. New data can be generated by sampling from this model. ↩
- 11. An informed prior is a distribution that adds information to the statistical inference by incorporating external knowledge. ↩
- 12. Vose Software. Informed Prior. Vose Software, 2017 (accessed January 27, 2020). ↩
- 13. Supra note 1. ↩
- 14. Supra note 2. ↩
- 15. The traditional non-Bayesian DM model uses these inputs: base lapse rate, PLT lapse rate, select and point-in-scale mortality, and an “effectiveness” parameter G, which represents the distribution of healthy lives and antiselectors between excess lapsers and persisters. The mortality of the persisters is then estimated using the concept of conservation of total deaths. ↩
- 16. Dukes, Jeffery T. Term Mortality and Lapses. Product Matters!, August 2005, (accessed January 27, 2020). ↩
- 17. Doll, Douglas C. Mortality Anti-selection—Different Versions of Dukes/MacDonald. Product Matters!, July 2003, (accessed January 27, 2020). ↩
- 18. Carpenter, Bob, Andrew Gelman, Matthew D. Hoffman, Daniel Lee, Ben Goodrich, Michael Betancourt, Marcus Brubaker, Jiqiang Guo, Peter Li, and Allen Riddell. 2017. Stan: A Probabilistic Programming Language. Journal of Statistical Software 76, no. 1:1–32. ↩
- 19. LOO and WAIC are standard tools used by data scientists and statisticians to measure out of sample accuracy (i.e., predictive capability) of the model. Colloquially, LOO estimates how well a statistical model can predict each member of the original data set, assuming the model was trained on all of the data except for the member being predicted. WAIC is a generalization of the Akaike Information Criterion (AIC) that analyzes model accuracy relative to how many parameters the model uses. ↩
- 20. Society of Actuaries. Lapse and Mortality Experience of Post-Level Premium Period Term Plans. Society of Actuaries, October 2009, (accessed January 27, 2020). ↩
- 21. Grid search allows for the search of all possible values, and G is selected to be equal to the point in the grid that most closely reproduces the observed number of deaths. ↩
- 22. Hoffman, Matthew D., and Andrew Gelman. The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo. Cornell University, November 18, 2011, (accessed January 27, 2020). ↩
- 23. Betancourt, Michael. A Conceptual Introduction to Hamiltonian Monte Carlo, July 16, 2018 (accessed January 27, 2020). ↩
- 24. Due to the sparse nature of the data, a multidimensional table (e.g., showing mortality rates for combinations of premium mode and risk class) could be misleading for the empirical analysis. Therefore, multidimensional results are not presented. However, the partially pooled model could give good estimates. ↩
- 25. Supra note 20. ↩
- 26. Vehtari, A., A. Gelman, and J. Gabry. 2017. Practical Bayesian Model Evaluation Using Leave-One-Out Cross-Validation and WAIC. Statistics and Computing 27, no. 5:1,413–1,432. ↩
- 27. ELPD and SED are standard tools used to measure the relative accuracy of the models using LOO and WAIC. The best model gets a score of 0 as it is being compared to itself. For the other models, the larger the magnitude of ELPD, the greater the divergence from the results of the best model. The SED gives a measure of confidence in the ELPD. ↩
- 28. Girosi, Federico, and Gary King. 2008. Demographic Forecasting, 66. Princeton: Princeton University Press. ↩
Copyright © 2020 by the Society of Actuaries, Chicago, Illinois.

