Creating Sustainable Regulation

Measures for reducing complexity in insurance operations

Bryon Robidoux December 2022

---

This article completes my series on the impact of complexity on insurance. Since the 2008 global financial crisis, the insurance industry has evolved rapidly. There has been a slew of new accounting rules and guidelines. Given the complexity of insurance companies, these changes have led to a relatively large amount of change in a short time. In my opinion, regulation ideally would provide maximum benefit and minimum burden to firms. As Albert Einstein said, “Everything should be as simple as it can be but not simpler.”

To understand how this may be achieved, in this article I will explain:

• The complex current state of the insurance industry
• The purpose of regulation and its consequences
• The four objectives of sustainable regulation and their measures

Ideally, this may allow us to combine measures to reduce complexity in the insurance industry.

THE COMPLEX CURRENT STATE OF THE INSURANCE INDUSTRY

As discussed in An Emerging Risk in 2022 (ER22), the insurance industry has become very complex, especially after the 2008 global financial crisis. As a result of that, we have seen many new regulations and accounting standards, including market-consistent ones. Market-consistent measures pump the fast-moving market environment through our books. Technology is changing faster, so organizations are creating more complex products to compete. As a result, we are under ever-increasing pressure to change.

Life and annuity companies have become massive and complex organizations. In Actuarial Modernization Errors, I explained that in my view, the long-dated nature of our promises, the vast array of disciplines required to work together and the stickiness of our processes make insurance companies slow to change. As alluded to in ER22, the slow pace of change in the insurance industry versus the fast-paced external environment can destabilize the industry. Among other goals, regulation and accounting intend to keep the industry stable, although they could be counterproductive in some ways. You might think years are long, but turning large organizations on a dime is challenging.

I am not stating that new regulation is unnecessary, but simply that the frequency of new regulation is high. I believe regulation is necessary and required. As I described in The Actuarial ‘Matrix’ and the Next Generation, I personally think the markets are inefficient. The “free market” has shown repeatedly that it is not efficient enough to solve complicated problems or deal with society’s issues. The conundrum is how to minimize the burden and maximize the effectiveness of regulation.

As part of the process for introducing new regulation, in my opinion, we want to use formal measurements to evaluate and understand the trade-offs of constructing regulations in various ways. By doing our best to optimize the trade-offs, we can create a more sustainable model of regulation and hopefully calm the changes coming from the outside environment.

THE PURPOSE OF REGULATION AND ITS CONSEQUENCES

I will define regulation’s purpose using my own words: Regulation primarily is concerned with creating rules to reduce the uncertainty of failure in an industry or firm. It mandates transparent communication of information to regulators and stakeholders. To dissect further, three critical concepts need to be clarified:

1. Uncertainty
2. Information
3. Transparent communication

Uncertainty

Uncertainty comes in two flavors: probability and possibility. Probability is only suitable for random events in a well-defined event space with well-defined, distinct events. An example is rolling a six-sided die. The event space is the six sides. The event is tossing a two; there is only one way to do it. Therefore, the probability is 1/6.

Uncertainty involves the possibility when there is any vagueness, such as lack of information or partial specification of the event or the event space. If your boss says, “We need to exceed or come close to last year’s sales figures,” then the chances of this occurring cannot be defined as a probability. As explained by Lodwick and colleagues, the terms “exceed” or “come close to” are indeterminant or vague, putting them in the possibility domain.¹

Vagueness is different from ambiguity. Ambiguity has multiple meanings that a sentence’s context cannot determine. It is unnecessary. Vagueness is more than an artifact of linguistics. It is inherent in our world. It helps reinterpret the Heisenberg Uncertainty Principle in quantum mechanics.² The natural world can never eliminate vagueness or be fully specified.

Possibility comes from a branch of mathematics called fuzzy mathematics. For brevity, it is a generalization of set theory. In set theory, an object either belongs to a set or it doesn’t. It is an all-or-nothing proposition. In fuzzy set theory, an object can partially belong to a fuzzy set. A statement can be both partially true and false.

Furthermore, a classic set from set theory is called a crisp set in fuzzy set theory.³ This is as far as I will go with the theory because this rabbit hole is deep. The important takeaways are the following:

• There is mathematics specifically designed to deal with vague concepts and linguistics.
• Vagueness is a type of uncertainty.
• Random events are not necessarily probabilistic.

Information

There is a connection between uncertainty and information. Assume I set up a random experiment. Before I performed it, there was average uncertainty because I didn’t know what would happen. After experimenting, I drain the uncertainty because I now have an answer. The average amount of information I gained from executing the experiment equals the uncertainty I exhausted. Therefore, uncertainty and information are two sides of the same coin.⁴

Transparent Communication

The communication process has the following steps:

1. A source, S, generates a message.
2. The encoder transforms data from the source into a signal.
3. It sends the signal through the noisy channel, CH.
4. The decoder receives the signal and reconstructs the message.
5. The destination, D, obtains the message.

The critical question in communication is: How much does the information in the output, Y, tell you about the input, X? In equation form, this is:

H(X,Y) = H(Y) – H(Y|X)

In the equation, you can read H as the average information. H(X,Y) is called mutual information, which is the average information in both the input and the output. H(Y|X) is the average information of the output given the input, which is called noise. So, to put it all together, mutual information is the average information in the output, less the noise.

Let’s talk briefly about noise. Because the average information and the average uncertainty are directly related, it is more intuitive to read H(Y|X) as the average uncertainty in the output given the input. Suppose the outcome has little to do with the input, even though the input was given. The lack of knowledge the input provides about the output means that there are a lot of distortions in the channel, i.e., noise. In other words, noise occurs when knowing the input tells you little about the output received.

Lastly, transparent communication is the same as mutual information. Therefore, noise reduction produces more transparency. Communication theory allows us to measure and minimize noise to deliver more clarity in financial results.

CREATING SUSTAINABLE REGULATION

It is my view that to be sustainable, regulation should consider the following objectives:

1. The Fisher Objective—regulation needs to record the current state and its risk and error metrics.
2. The Shannon Objective—regulation should transmit the most information with the least amount of noise to the regulators and stakeholders.
3. The Zadeh Objective—regulation must balance indeterminacy with specificity to maximize speed and accuracy of understanding as well as consistent implementation of the rules.
4. The Kolmogorov Objective—regulation must keep the time and complexity of the implementation, calculation and operation within predefined tolerances for both humans and machines.

Meeting the Fisher Objective

As I explained in The Actuarial ‘Matrix’ and the Next Generation, accounting for a stochastic world is difficult. Expected values and point estimations tend to remove vital information to help determine an organization’s current state and going concerns. In my opinion, we live in a complex, stochastic, deterministic world, all bundled together and inseparable. To accurately account for the variability in the world, according to certain schools of thought, we would need to add statistics to accounting, which experts call “stochastic accounting.”

Fisher information is the probabilistic concept that statistical models are a mode of transferring information about variability in parameters and results.⁵ It is the typical way finance and statistics define uncertainty. Furthermore, it can measure the confidence intervals, parameter sensitivity and propagation-of-error metrics for the projected assets and liabilities. Fisher information will improve regulation, in my view, by accounting for noise sources in the estimations. It is just as important to understand the noise and its origins as it is to understand the point estimates themselves.

Regulation is intentionally “conservative” in the sense of involving moderation, like using fixed interest and mortality rates in the United States. Without the statistics in financial reports, determining what moderation or caution would involve would be difficult without relying on subjective judgment. What a small company may view as a moderate, cautious approach may be vastly different for a massive company. Furthermore, regulations get stale. What was cautious in yesterday’s environment may not be the same in today’s environment. It would achieve greater consistency, in my view, to base regulations on statistical properties of a company’s business and its environment rather than a one-size-fits-all table of values.

Meeting the Shannon Objective

Even after actuaries report their numbers and the variations around the estimates, there is still noise and uncertainty to address. To meet the Shannon Objective, we would need to measure the amount of noise generated by different rules to increase the mutual information between source and destination.

The noisiest regulations would require running a single scenario, a heuristic that would allow regulators to assess the financial health of an organization quickly. I do not envy regulators because their job description is to drink from the firehose perpetually! Unfortunately, Hardy has demonstrated that these single scenarios are almost all noise and provide limited value⁶ because the input scenario says little about the likely best-estimate outcomes.

Meeting the Zadeh Objective

Now it is time to move on to possibilistic uncertainty related to indeterminacy or vagueness. Indeterminacy must balance specificity, as shown in Figure 1. Vagueness occurs when writing rules with partial or incomplete details to try to cast a wider net to capture more situations. It leads to loopholes. According to Kades, the loopholes cause dynamic complexity because regulators want to fill them and firms want to exploit them,⁷ which is a vicious cycle. Specificity plugs loopholes by creating more technical complexity. Kades explains that technical complexity is the difficulty in understanding and implementing the regulation.⁸

In my opinion, finding the sweet spot between dynamic and technical complexity may improve regulation. The sweet spot is where the industry maximizes the understanding, so practitioners would have a higher chance of consistent implementation. Finding the sweet spot would involve measuring how vague the rules are within the regulation. Luckily Measuring Vague Uncertainties and Understanding Their Use in Decision Making⁹ describes a statistical method for querying experts on the vagueness of different language terms, which helps define the degree of membership the language terms have to various sets. Wallsten explains that statistical processes are advantageous because the experts’ judgments are different and contain noise.¹⁰ This noise has many interesting consequences, as shown in Figure 2.

According to Fuzzy Communication in Collaboration of Intelligent Agents, indeterminacy is critical to increasing communication by minimizing the amount of information sent between intelligent-agent robots. These robots must have all their codebooks and contextual knowledge on board and synchronized. The more these conditions are relaxed, the less efficient and more difficult it is to coordinate the robots because they must increase their communication specificity significantly.¹¹ This specificity increases the volume of information pumped through the channel, which reduces the speed at which the robots can coordinate, as shown in Figure 3.

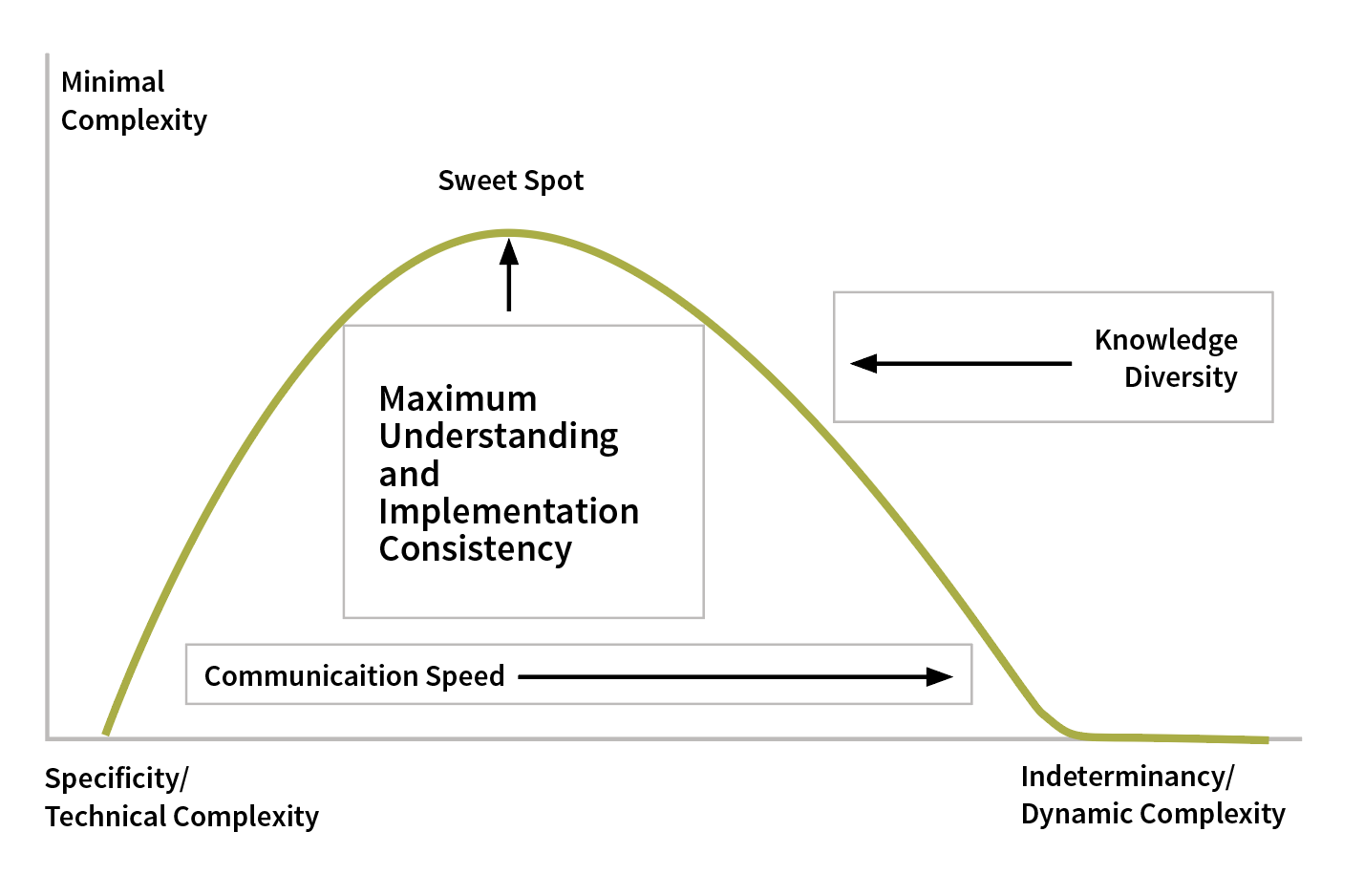
Why do I care about robots? Because, in my opinion, they create a scenario of maximum efficiency that humans cannot replicate. Humans suffer the same mechanics as robots, but in my view, they are significantly less efficient. The robots’ codebooks and contextual knowledge are equivalent to human knowledge and know-how, but robots can have complete uniformity in their expertise and know-how. Unless everyone lives in the movie The Truman Show, there is no way to control consistency between life experiences and knowledge base for humans.

This reality implies that the sweet spot is a moving target, but its stability relies on uniformity. Knowledge diversity will right-skew the distribution in Figure 3 and move the sweet spot toward technical complexity and more specificity.

One fascinating result is that diversity is the friction of efficient communication and is required to evolve new ideas. Inefficiency and evolution go together! The noise of the experts is related to the diversity of their experiences. It is easy to see why law and regulation are so messy and challenging—everyone involved has vast differences in knowledge, know-how and experience.

Meeting the Kolmogorov Objective

Even after all the uncertainty is addressed, sustainable regulation likely would want to consider the complexity of implementation. How lawyers and judges interpret laws is notoriously noisy due to all kinds of cognitive limitations. According to Kahneman and colleagues, to address ideas of fairness, justice, product complexity and comfort in heuristics creates even more complicated laws and regulations.¹² There is a spiderweb of interrelated laws and regulations that can lead to contradicting conclusions and circular logic.

The theories of computability and complexity theory can help and are closely related. In complexity theory, the goal is to classify problems as easy or hard to solve. In computability theory, the objective is to organize problems as solvable or unsolvable.¹³

As reported in The Laws of Complexity and the Complexity of Laws: The Implications of Computational Complexity Theory for the Law: “To the extent that multifaceted notions of justice lead us to draft complicated rules, [computational complexity theory (CCT)] tells us when our desire for justice crosses the threshold from practicality to impracticality. In addition to ‘narrow’ applications that show when legal rules are unworkable for cases of significant size, CCT provides insights into more general issues of what is legally complex and why. [I]t [can] show that some existing legal rules are indeed impractical in bigger cases.”¹⁴

By using the methods of computer science and the theory of computation, I believe we could analyze the practicality of the regulations and the trade-offs among different designs. We could understand the complexity in its description and the time required to compute the law, as some scholars did with Dodd Frank.¹⁵ In my opinion, we could benefit by striving for regulation that requires the least amount of time and memory constraints to meet the overall objective, both on the human and machine fronts. In my opinion, compressing regulations and practices to make them as manageable as possible with just the right amount of complexity may have great benefits.

CONCLUSION

To reduce the complexity of the insurance industry, we ideally would devise regulations that supply the maximum benefit with the minimum burden—have rules that are complex enough to meet their goals though not any more complex. To accomplish this, I suggest we attempt to meet four objectives: Fisher, Shannon, Zadeh and Kolmogorov.

1. The Fisher Objective would necessitate using statistics in our reporting, to define caution and moderation based on reported statistics and to handle the uncertainty inherent in the financials, which point estimates tend to hide.
2. The Shannon Objective would require us to maximize transparency in our financials by minimizing rules that produce noise and unhelpful heuristics. U.S. regulators are overwhelmed with data—it makes sense to simplify their jobs and steer away from noisy, irrelevant content.
3. The Zadeh Objective would require measuring the vagueness in our rules to maximize understanding of intent and consistency of implementation. My hope is that this objective may reduce regulatory change frequency because it would potentially reduce the available loopholes. The ironic and troubling result is that, in my opinion, knowledge diversity works against this objective.
4. The Kolmogorov Objective’s implementation would measure regulation’s machine and human computation complexity. This measurement potentially may allow an understanding of the trade-offs in different implementations. The goal would be to minimize the computation required of both humans and machines.

Requiring all regulations to measure and optimize these objectives means it will take longer to implement them. Nevertheless, to me it seems like one way to ease the ever-growing complexity of supplying insurance. As complexity increases, so too does the cost of providing insurance. By creating sustainable regulation, we may reduce cost and complexity, and as a result, more customers may benefit from insurance products.

Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries or the respective authors’ employers.

Copyright © 2022 by the Society of Actuaries, Chicago, Illinois.