Hedge Your Bets

Insurance companies utilize derivatives in a variety of ways to manage and mitigate risks that are inherent in their investment or liability portfolios. This can be anything from traditional asset/liability matching to mitigate interest rate risk, to dynamic hedging that targets multiple risk factors associated with the liabilities, and static hedging that targets major enterprisewide exposures over long-time horizons.

Life insurance liabilities can be characterized by three main features: long-term duration, large volumes and significant market risk exposure. Specifically, guaranteed minimum income and withdrawal benefits greatly increase insurers’ risk exposure to market volatility, while pension and other post-retirement benefits could be hurt if equity returns fall short of expected long-term rate-of-return assumptions.

Given the persistent low interest rate environment across the curve since the 2008 financial crisis, insurance companies need hedge assets, as illustrated by the significant recent increase from $786 billion as of fiscal year 2010 to $1,885 billion as of FY 2014. In that respect, the use of downside protection options is appropriate. However, buying large hedge portfolios requires taking into account transaction size explicitly, including market impact, because equity derivatives are highly sensitive to supply/demand balance. The primary tools used by insurers in 2014 were put options (44 percent, versus 24 percent for calls). Ninety percent of these put options were purchased, implying the growing cost of hedging.

Using derivatives to hedge financial risks embedded within insurance liability guarantees

Life insurers write long-dated guaranteed policies and attempt to hedge these guarantees using hedge assets (e.g., futures, options). As the guarantees embedded within the insurance liability hold a convex risk profile with respect to the underlying stock, insurance companies need to buy some convex equity hedge assets such as options (in contrast to linear instruments like futures) in order to match the liability risk profile to improve hedge effectiveness.

Solvency II is expected to strengthen the issue of hedge derivatives liquidity

There already has been significant evidence of illiquidity cost stemming from supply-and-demand imbalance for options, which Solvency II is expected to further strengthen as insurers will be forced to hold sufficient capital to remain solvent during periods of market stress. Solvency II aims to match insurance capital requirements with the economic risks embedded within the long-dated liability guarantees, which insurers used to hedge through, rebalancing cheap equity futures dynamically in contrast to costly static options.

However, futures are not given full credit under Solvency II (as stress is applied instantaneously rather than over a period of time), thus putting pressure on insurance companies to buy large quantities of options where prices will increase as a result of supply-and-demand imbalance.

Integrating market impact into large hedging transactions

As a result, an explicit modeling of such increasing cost of options is made through a market impact function, the influence of which the insurance company will try to minimize. In this context, best execution cannot be defined as a single number within a single trade. Rather, the market impact on the option price depends on “temporary impact strength” that is proportional to the main empirically observed drivers: the speed of option trading (i.e., number of options per unit of time), the equity stock level and the option sensitivity to the equity stock.

Optimal hedging transactions significantly depend on the risk appetite

Consider a life insurance company aiming to minimize the cost of buying a large quantity of put options to hedge liabilities. Such a strategy will depend on specific risk appetite, such as a maximization of the mean profit/loss objective (or minimization of the mean cost of buying options), or a risk-reward objective including the minimization of the dispersion of the profit and loss. The standard procedure of the Hamilton-Jacobi-Bellman (HJB) framework in stochastic control problems is applied, coupled with numerical schemes.

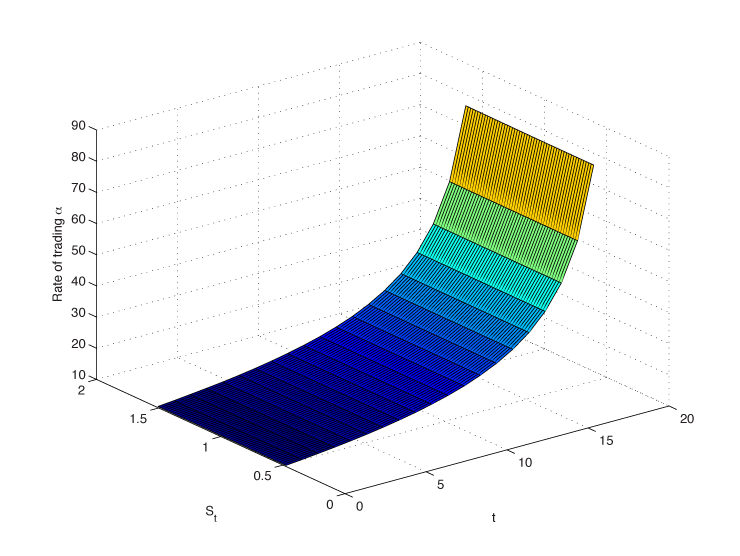
To maximize mean profit/loss, the optimal execution strategy provides a rather stable pace of trading as illustrated in Figure 1, depending only mildly on the stock price path. The pace is rather constant at the beginning and then gradually increases as it gets close to maturity, which is intuitive given the fixed quantity to buy within a fixed time period, implying the insurer must acquire at a faster rate as time passes.

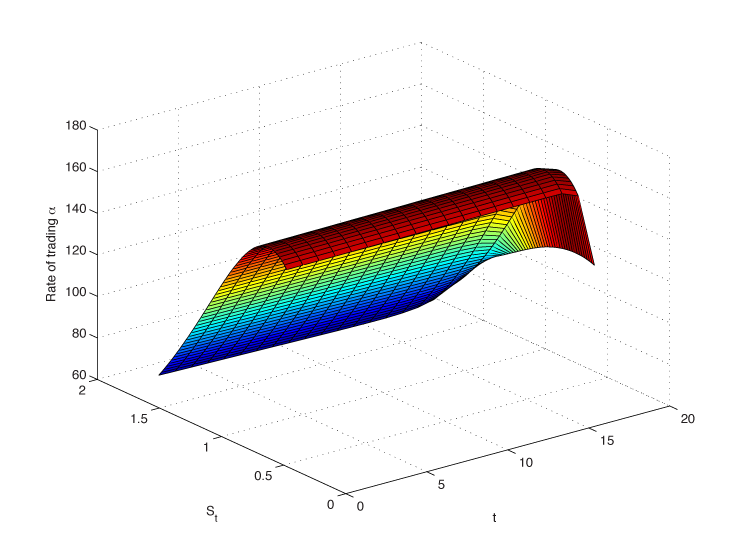
In contrast, if the dispersion of the profit/loss becomes an additional driver of the risk appetite, then the optimal execution strategy significantly depends on the stock path, with a faster pace when the stock level is low compared to when the stock level is high (as illustrated in Figure 2). Indeed, as the stock decreases, the cost of the put option increases. The optimal execution strategy also depends on the impact of the option volume trade on the option cost. One needs to trade as soon as possible in order to minimize the hedge transaction cost. The opposite is true if the stock market rises. The mean-variance profit/loss framework prevents the insurance company from waiting until maturity to trade a large quantity and instead favors a decreasing trading pace as time passes.

Conclusion

Within the mark-to-market valuation framework under Solvency II, the size of hedging transactions may put significant constraints on an insurance company because of the higher cost of hedging liabilities that stem from their market impact. In that respect, the risk appetite has significant influence on the optimal transaction execution path.