Smart Shopping

Imagine you are contemplating buying your next suit. The first question in your mind is probably “bespoke or off-the-rack?” The same question arises when the time comes to choose a pension de-risking solution. Broadly speaking, pension de-risking solutions can be divided into two categories: bespoke (indemnity-based) and off-the-rack (standardized).

Bespoke Solutions

Bespoke solutions are based on the actual mortality experience of the hedger’s own portfolio. They typically are executed with (re)insurers in the form of buy-ins (through which the asset and liabilities of a pension plan are transferred to an insurer), buy-outs (through which bulk annuities are acquired to pay pensions) or customized longevity swaps (through which fixed cash flows are exchanged for floating cash flows that depend on the actual mortality experience of the hedger’s portfolio).

Figure 1 illustrates the mechanism behind a customized longevity swap. During the term of the swap, the pension plan (the hedger) will swap pre-agreed monthly payments with the counterparty (a reinsurer) in return for monthly payments dependent on the longevity of the plan’s own members. Should the plan members’ mortality be lighter than expected, the pension plan would receive net payments from the reinsurer that could then be used to offset the corresponding higher pension payouts.

By its definition, a bespoke solution provides a perfect hedge. There is no residual risk about which to worry.

Off-The-Rack Solutions

Alternatively, a pension plan may choose to de-risk with off-the-rack (standardized) solutions. Standardized solutions typically are executed in the form of capital market derivatives, which are linked to broad-based mortality indexes rather than the mortality experience of the hedger’s own portfolio of individuals. The following sections describe examples of such derivatives.

q-Forward

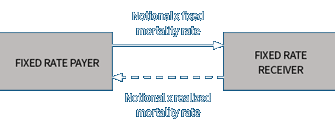
A q-forward is a zero-coupon swap that exchanges at maturity an amount proportional to the realized prevailing mortality rate at a certain age (the reference age) with an amount proportional to a fixed mortality rate.¹ To hedge longevity risk, a pension plan should participate in a q-forward as a fixed-rate receiver so that it would receive a net payment from the counterparty when mortality turns out to be lighter than expected (i.e., when its liability is higher than expected). Figure 2 illustrates the exchange of cash flows in a q-forward.

S-Forward

S-forwards are identical to q-forwards, except they are linked to cohort survival rates instead of mortality rates.² S-forwards are regarded as more sophisticated than q-forwards, because a cohort survival rate is a function of multiple mortality rates at multiple time points.

K-Forward

Recently, a conceptual mortality derivative called K-forward has been proposed.^3,4 A K-forward has the same structure as a q-forward, but it is linked to a “parametric mortality index” constructed using a time-varying parameter in a robust stochastic mortality model. One advantage of K-forwards is that a parametric mortality index is able to capture more information concerning the evolution of mortality than traditional, nonparametric indexes, such as mortality rates and survival rates.

Longevity Experience Options

Longevity Experience Options (LEOs) are out-of-the-money call options on forward survival rates. Deutsche Bank reportedly executed the first LEO with an insurance-linked securities fund in 2013.⁵

Of course, standardized solutions do not offer a complete elimination of longevity risk. The hedger is subject to certain residual risks that must be managed by other means.

Why Off-The-Rack Makes Sense

We all love the process of getting a bespoke suit, from the first consultation to the delivery of the end product that fits perfectly. But let’s face it; a bespoke suit is not exactly inexpensive.

The fact that off-the-rack is generally less costly than bespoke applies not only to clothing, but also to financial instruments due to the fact that off-the-rack financial instruments are more liquid. As discussed in one of our previous papers,­⁶ there exists profound evidence for an inverse relationship between liquidity and Sharpe ratio (a measure of the compensation to investors who accept the risk entailed) in stock, mutual fund and hedge fund markets. It has been argued that the market for longevity risk transfers is highly akin to a typical financial market,⁷ so it is reasonable to conjecture that off-the-rack longevity hedges are more economical than bespoke ones.

Cost is not the sole factor. In today’s market, there are not enough tailors (insurers providing bespoke de-risking solutions) to meet the demand for longevity risk transfers. Using the assets for pension plans (in excess of 31 trillion USD) as a proxy for demand and the assets held by the global insurance industry to cover nonlife risks (2.6 trillion USD) as a proxy for supply, George Graziani⁸ from Swiss Re concluded that the demand for acceptance of longevity risk exceeds supply by a multiple of 10. Experts from Société Générale⁹ also reached a similar conclusion by comparing the potential increase in pension liabilities due to unforeseen longevity improvement with the aggregate capital of the global insurance industry. Therefore, there is a need to invite capital market investors to take longevity risk exposures (in exchange for a risk premium). Such investors prefer off-the-rack to bespoke, because the former is free of the information asymmetry arising from the fact that hedgers (pension plans) have better knowledge about the mortality experience of their own portfolios.

Getting The Right Off-The-Rack Longevity Suit

When shopping for an off-the-rack suit, you find the one that best matches your body in terms of waist, chest, shoulder and so on. Likewise, when building a longevity hedge with off-the-rack mortality derivatives, you need measurements of the longevity risk exposure of your portfolio. These measurements can be defined from two different angles:

• Treating the mortality curve as an interest rate yield curve, or
• Applying an analogy between longevity risk and equity risk.

Method 1: Treating the Mortality Curve as an Interest Rate Yield Curve

Interest rate risk and longevity risk share heaps of similarities:

• Both interest rates and mortality rates have “term structures.” Interest (yield) rates on zero-coupon bonds vary with time-to-maturity, while mortality rates vary with age.
• Both interest rate yield curves and mortality curves evolve over time in a random manner.
• Shifts in interest rate yield curves and mortality curves are generally not parallel.

Given these similarities, it makes a lot of sense to measure exposures to longevity risk using metrics that are parallel to interest rate duration and convexity. A metric called “key q-duration” was developed along this line.¹⁰

More specifically, a key q-duration measures the sensitivity of a life-contingent instrument/liability to a specific portion of a mortality curve. It is largely analogous to “key rate duration,” which has been used extensively by traders to measure and manage interest rate risk.

One can find the best-fitting portfolio of off-the-rack mortality derivatives by matching the key q-durations of the hedge portfolio and the liability being hedged. It has been demonstrated that under idealized assumptions, a hedge calibrated using the method of key q-duration can eliminate more than 90 percent of longevity risk (in terms of variance reduction).

Method 2: Applying an Analogy Between Longevity Risk and Equity Risk

When measuring the risk entailed in a stock option, Greek letters often are used. A Greek letter measures the sensitivity to a specific parameter in an option pricing model. For example, delta measures the first-order sensitivity to S₀ (the time-0 value of the underlying asset) and gamma measures the second-order sensitivity to S₀.

Analogously, one may measure exposures to longevity risk using “longevity Greeks,” which gauge the sensitivity to changes in certain parameters driving the evolution of mortality in the stochastic process. Of particular importance is the time-varying parameter (the period effect) in the assumed stochastic mortality model. Longevity delta and gamma have been defined to capture the first- and second-order sensitivities to this parameter, respectively. By matching longevity Greeks, one can easily formulate an optimal portfolio of off-the-rack mortality derivatives.^11,12

Recent Contributions to Greek Hedging of Longevity Risk

At the 2017 Society of Actuaries (SOA) Living to 100 Symposium, we presented a paper that investigates various aspects of Greek hedging of longevity risk.¹³ The following points are the key findings of the paper.

The evolution of mortality over time is subject to stochastic volatility (see Figure 3). For this reason, it is important to include the sensitivity to volatility when measuring longevity risk exposures. To this end, we have introduced a new metric called “longevity vega” and demonstrated its usefulness in hedging longevity risk.

We derived semi-analytical formulas for calculating longevity delta, gamma and vega from an extension of the Lee-Carter model. The calculation does not require finite differencing and is therefore not computationally demanding.

We derived and explained the properties of the three longevity Greeks for q-forwards with different specifications. As with developments for equity options, these properties allow us to know more about q-forwards as a risk mitigation tool. In practice, when a perfect Greek neutralization is not always possible, these properties also can guide the hedger to choose an appropriate q-forward that can offset his or her longevity risk exposure in a particular dimension. For instance, if the hedger has an annuity liability with a large longevity gamma, then based on our results he or she should contemplate acquiring a q-forward with a high reference age.

Using the properties of longevity Greeks, we identified and explained several relationships between hedge effectiveness and q-forward specifications. The results reveal several interesting facts. For example, in a delta-vega hedge formed by q-forwards, the choice of reference ages does not materially affect hedge effectiveness, but the choice of times-to-maturity does. This may aid hedgers to better formulate their hedge portfolios in terms of choosing which q-forwards to use and which longevity Greeks to match.

We validated our Greek hedges using a nonparametric bootstrapping method that does not depend on any model. As expected, the hedge effectiveness is somewhat reduced when the model assumption breaks down, but many of the theoretical relationships between hedge effectiveness and q-forward specifications are still observed, even when the evaluation scenarios are generated by a model-free approach.

Conclusion

In summary, off-the-rack longevity hedging solutions offer an attractive alternative to bespoke ones. To ensure that a portfolio of off-the-rack mortality derivatives fits, one can rely on measurements such as key q-durations and longevity Greeks. Our recent results about longevity Greeks give hedgers a better understanding on what fits them well—and what does not.

Other than the search for a good fit, there are several issues surrounding off-the-rack longevity hedging solutions, including population basis risk that arises from the difference in the mortality experience between the hedger’s portfolio of individuals and the population to which the mortality derivative used is linked. These issues are not discussed in this article, but are investigated extensively in a few academic papers.^14,15

Researchers are now working hard on the topic of standardized mortality derivatives, with a goal of helping you be a smarter suit shopper.