Tontine Thinking

Author’s Note: This article includes preliminary material from a research effort on tontines (conducted with various colleagues and students at York University), co-sponsored by the Society of Actuaries (SOA). Tontine annuities were introduced as fiscal instruments of public borrowing in the late 17^th century and then morphed into a form of speculative investment during the 18^th century. After some undesirable mutations by the (American) insurance industry, tontines fell into disrepute in the late 19^th century and were eventually banned by regulators in many legal jurisdictions around the world by the mid 20^th century. In this article, I discuss whether the retirement challenges of the 21^st century create an opportunity for their reintroduction. Actuarial science, regulation and technology have progressed considerably since the 17^th century, and nobody (in their right mind) would propose recycling the original scheme promoted by Lorenzo de Tonti. Rather, this article makes the case for what I call “tontine thinking”—or making mortality credits transparent and explicit—in the design of retirement income products of the future.

In the year 1693, the government of England was struggling with the cost of an expensive and unpopular war against France and was looking for an innovative way to finance its expenditures and budget deficits at the lowest possible interest cost and rate. Recall that this was a financial era before long-term bonds or central banks. So, the English decided to try a rather risky strategy, borrowing an idea that recently had been attempted in France (ironically) to finance its war against the English. An act of Parliament was passed that approved the borrowing of £1,000,000 (which today might be worth 100 to 200 times that amount) via something we would now call a tontine annuity—the impetus for this article.

Basically, the government offered a syndicate of wealthy lenders 10 percent interest for seven years and then 7 percent interest in perpetuity, all in exchange for the £1,000,000. But the principal would never be returned.  Thus, for example, in the year 1694 (after one year) the Exchequer would make £100,000 in total interest payments to the syndicate of lenders. The same process would be repeated in 1695, 1696 and so on. Then, in the year 1700, the annual interest payments to the syndicate would be reduced from 10 percent to 7 percent, which is a total outflow of £70,000 per year until the syndicate is gone—defined in a moment. The arithmetic is all pretty basic, but it is notable for being one of the earliest attempts at long-term borrowing in England.

The catch here—or the difference between this fixed-income instrument and any other perpetual coupon bond issued in the last 300 years—is that the annual interest payments would only be distributed to the investors in the syndicate conditional on their original nominee being alive. To clarify here, in the year 1693 when the loan was syndicated, anyone (e.g., the annuitant) who lent or invested £100 (the minimum investment) via this scheme had to select a nominee upon whose life the interest payment would be continued. If and when the nominee died, the payments ceased to the annuitant. As one might expect, the nominees to the 1693 tontine were (mostly) young healthy children—the average age of the typical nominee was 10—who were expected to live long lives. But, of course, not all of them did in practice. Some of the earliest mortality tables in England were based on the experience of this group of nominees.

So, for the sake of example, assume that 10,000 annuitants each invested the minimum £100 in the scheme and selected 10,000 distinct nominees. Assume also that by the year 1697, a total of 500 of the nominees had died during the first four years of the scheme. Then the £100,000 of interest for the year 1697 would be distributed among the corresponding 9,500 annuitants, which would result in a dividend of 100,000/9,500 = £10.53 per annuitant (again, whose nominee was still alive). Actuaries will recognize immediately that the £0.53 more than the guaranteed 10 percent interest were mortality credits. Although at the time they were called benefits of survivorship.

Now, fast-forward a quarter of a century. If by the year 1720—incidentally the year of the famous South Sea stock market crash—a hypothetical total of 4,000 nominees had died, then the £70,000 in interest would be distributed to 6,000 annuitants, generating a dividend of £11.67, which can be broken down into 4.67 percent (or £4.67) of mortality credits plus 7.00 percent (or £7.00) of interest. Recall that by construction and design, in the year 1700 the aggregate interest payment to the syndicate was reduced from 10 percent to 7 percent, which leads to a lower numerator. This pattern would continue until the last remaining survivor (nominee) received a dividend of £70,000 until she died, and the tontine was extinguished. Well, that was the plan—at least in broad brushstrokes. In some sense, one can think of this as a type of “lapse-supported” insurance product enabling the issuer to price using a “better” interest or discount rate, although obviously once the original tontine investment is made there is no point in lapsing. You might as well hold on while your nominee is still alive.

In practice, the 1693 tontine annuity wasn’t fully subscribed, perhaps because investors at the time had better alternatives and a famous astronomer by the name of Edmond Halley counseled against the tontine.¹ The oldest nominee linked to the 1693 tontine was a female who died in 1783 at the age of 100. Yes, she was selected as a nominee at the age of 10. My point here isn’t to tell the full history of the first English tontine loan, but rather to unearth possible lessons or ideas for the retirement income products of the future.

The Retirement Challenge

With the global decline in defined benefit (DB) pension coverage and the increase in defined contribution (DC) investments—a phenomenon that has been debated and discussed at length—there is also a growing concern among policymakers that retirees of the future will no longer have access to low-cost and efficient longevity pooling schemes (i.e., the actuarial backbone of DB plans). This problem is exacerbated by what financial economists call the annuity puzzle, which is the reluctance of older consumers to voluntarily use money or funds from their nest eggs to purchase life-contingent annuities, despite their welfare-enhancing properties. Either way, by choice or by design, generic DC schemes “rob” retirees of mortality credits and the benefits of pooling. This then reduces retirement sustainability, which already is hampered by an era of low (real) interest rates, increasing longevity and reduced discretionary savings. Indeed, these facts are all well-known to specialists. The question is whether centuries-old tontines—or at least the underlying DNA of a tontine—can help. I believe the answer is yes.

Elements of Tontine Thinking

The original 1693 design that I described—and what has been named King William’s tontine by historians, since he was the reigning English monarch at the time—can inspire future generations of DC retirement income products with what I call “tontine thinking.” In particular, there are four elements of King William’s tontine that are worthy of consideration.

Less Capital Intensive

Unlike a pension plan or annuity company, the issuer of a tontine annuity doesn’t incur much longevity risk. The borrower or issuer makes known fixed payments (the numerator), which are distributed among the survivors (the denominator). The group or syndicate incurs aggregate longevity risk, not the borrower. This then reduces the need for capital (if it was an insurance company) and in theory would increase the expected payout per survivor.

Now, just to be clear, the sponsor does face some modicum of risk in having to forecast whether the one last surviving nominee will live 50, 55 or perhaps 60 years. However, the discounted present value of that (uncertain) liability ending date pales in comparison to the longevity risk faced by pension plans of insurance companies that only sell annuities. Ergo, the lower (or nonexistent) capital requirements should result in better payouts for annuitants and retirees—in exchange for incurring aggregate longevity risk.

Complete Transparency

Anyone who participated in the 1693 tontine annuity knew exactly why he or she was receiving a particular dividend in a particular year. The calculation could be done—and was actually reported—on a single sheet of paper that is still preserved today in the archives of the British Library in London. The cash-flow numerator was known in advance, and the denominator of survivors easily could be counted every year at the designated dividend date. The division of the two numbers didn’t require any advanced mathematics or actuarial discretion. One certainly didn’t require a 2,000-page legal prospectus to explain to (novice) investors the ins and outs of caps, floors, ratchets and roll-ups. It didn’t leave anything to the discretion of actuaries.

Real Longevity Insurance

Like all life-contingent annuities, the tontine annuity would protect the investor against the nominees—which could also be the investor—living longer than they had originally planned or anticipated. The longer they lived, the more income they received. The last few survivors—who by definition had lived very long lives—would receive larger payments, which then (might) serve as a hedge against uncertain medical expenses that (might) increase at a rate higher than inflation. In some sense, nominal instruments were being used to generate real returns. This is a subtle point that is worth repeating. If shocks to population mortality are correlated with shocks to the state of the economy—in other words, they are not statistically independent processes—the tontine’s redistribution mechanism might have utility enhancing properties.²

Payments Increase Slowly

One of the interesting features of the 1693 (Williamite) design was the one-time reduction in interest payment to the syndicate. Recall that for the first seven years the interest rate was 10 percent, and then in the year 1700 it was reduced to 7 percent. This design element differed from the original Lorenzo di Tonti (French) scheme under which the interest paid to the group was constant over the entire horizon. Notice then that as the denominator (survivors) was expected to shrink, the numerator would decline as well, and thus result in levelized payments.

This idea can be extended from a one-time adjustment to a constant reduction in cash flows. In theory, the sponsor could construct a tontine annuity using zero coupon bonds in which the cash flows (numerator) decline at roughly the same rate as the denominator. In some technical work I published with Tom Salisbury,³ we call this a natural (aka levelized) tontine. Figure 1 displays a confidence interval for payments or income over time. On average, payments remain constant, but there is a positive skew in the cash flows—the fingerprint of a tontine—which means that long-lived retirees might receive (very) large payments at the risk of only a modest decline if aggregate longevity was lower than expected.⁴

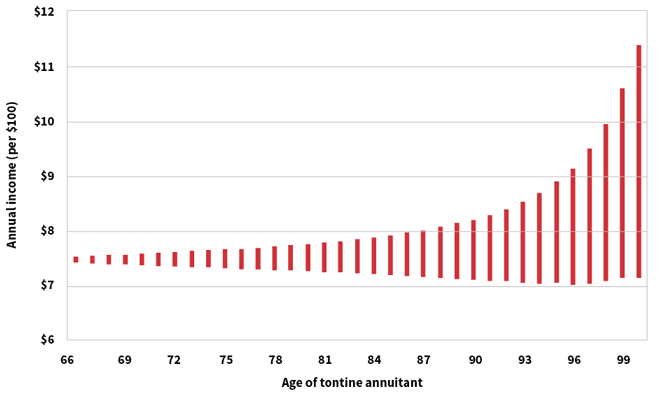
The design of such “pooling” arrangements—where aggregate longevity risk is shared among a group and not incurred by the issuer—is a fertile area of academic research, and other authors^5,6 have proposed alternative designs. In fact, in an ongoing research project co-sponsored by the SOA, my co-researchers and I are:

1. Conducting (historical) Monte Carlo simulations to examine how a natural tontine would compare to payouts from conventional annuities, and
2. Quantifying the utility benefits of natural tontines versus annuities in the presence of background economic risk, such as unexpected medical inflation.

Preliminary evidence suggests that a suitably immunized (or collateralized) tontine annuity might offer 10 percent to 15 percent more income and/or utility value (at retirement age 65) compared to a life annuity.

Of course, there is some “risk,” which is clearly displayed in Figure 1. Payments could indeed decline. In fact, the underlying probability and statistics required to model the next generation of tontine annuities are well understood and part of the current canon of actuarial theory. Indeed, ​a Ph.D. in rocket science isn’t needed or required to resurrect tontines.

The real challenges would be legal and regulatory rather than scientific. First, the current annuity and insurance industry might be reluctant to concede high-margin products. Next, there are skeptical regulators to win over—perhaps the grandchildren of state insurance commissioners who banned tontine insurance a century ago—and they might not take kindly to anything with the word tontine in the title, regardless of exact substance or economics. These words matter to lawyers.

Final Thoughts

While the idea of reintroducing a tontine-like structure as yet another retirement product on the menu might seem natural to actuaries, I can personally testify that many members of the public—as well as media, plan sponsors and especially politicians—recoil in horror when tontines are explained to laymen, especially if it is done tactlessly. One well-known financial writer and author⁷ has described tontines as “the most discredited financial instrument in history.”

The principal objection—again, anecdotally—appears to be the direct benefit a surviving investor receives from the immediate death of a member of the original syndicate (or their nominee). Some commentators go so far as to worry about nefarious moral hazard concerns. Of course, the transfer of assets from deceased to survivors, and vice versa, is at the heart of all social insurance systems, albeit perhaps not as transparently. Moreover, the identity of participants and even the entire transfer process can nowadays be made anonymous (via Blockchain) online, although I certainly understand the reluctance to embrace any company’s claim that its online data is 100 percent secure and anonymous in perpetuity.

Then, in addition to what some call the ethical dilemma, there is also an aversion to an insurance product with no legacy or bequest value—although that also can be corrected in the design, at the expense of reduced mortality credits. Alas, actuaries of the 21^st century already have a ready-made solution to all these problems, but as the annuity puzzle I described can attest, the optimal retirement income product isn’t necessarily a very desirable or popular one. More often than not, the suboptimal strategies and products (paying the highest commission) are most widespread.

But to end this article on a positive and behavioral finance note, perhaps once retirees are shown the extreme (naked) version of mortality credits and risk pooling—and they reject it after properly thinking it through—they are more likely to embrace the tontine’s tamer cousin on the menu; namely, the life annuity in which income is guaranteed, smoothing risk is reduced and the impact of death isn’t as obvious. As all good sales and marketing professionals have learned, it helps to have an “over-the-top” product advertised next to the item you really want to sell. Walk into any jewelry store, and you will see what I mean. So perhaps the 17^th century tontine can be resurrected as a behavioral anchor that nudges people into generic annuities. Well, that is the theory, at least.